# 图

在计算机科学中，一个图就是一些顶点的集合，这些顶点通过一系列边结对（连接）。顶点用圆圈表示，边就是这些圆圈之间的连线。顶点之间通过边连接。

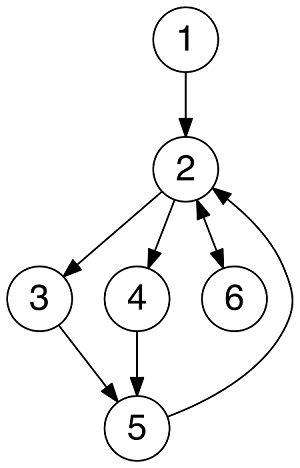
# 什么是图

• 阶（Order） - 图 G 中点集 V 的大小称作图 G 的阶。
• 子图（Sub-Graph） - 当图 G'=(V',E') 其中 V‘包含于 V，E’包含于 E，则 G' 称作图 G=(V,E) 的子图。每个图都是本身的子图。
• 生成子图（Spanning Sub-Graph） - 指满足条件 V (G') = V (G) 的 G 的子图 G'。
• 导出子图（Induced Subgraph） - 以图 G 的顶点集 V 的非空子集 V1 为顶点集，以两端点均在 V1 中的全体边为边集的 G 的子图，称为 V1 导出的导出子图；以图 G 的边集 E 的非空子集 E1 为边集，以 E1 中边关联的顶点的全体为顶点集的 G 的子图，称为 E1 导出的导出子图。
• 有向图 - 如果给图的每条边规定一个方向，那么得到的图称为有向图。
• 无向图 - 边没有方向的图称为无向图。
• 度（Degree） - 一个顶点的度是指与该顶点相关联的边的条数，顶点 v 的度记作 d (v)。
• 入度（In-degree）和出度（Out-degree） - 对于有向图来说，一个顶点的度可细分为入度和出度。一个顶点的入度是指与其关联的各边之中，以其为终点的边数；出度则是相对的概念，指以该顶点为起点的边数。
• 自环（Loop） - 若一条边的两个顶点为同一顶点，则此边称作自环。
• 路径（Path） - 从 u 到 v 的一条路径是指一个序列 v0,e1,v1,e2,v2,...ek,vk，其中 ei 的顶点为 vi 及 vi - 1，k 称作路径的长度。如果它的起止顶点相同，该路径是 “闭” 的，反之，则称为 “开” 的。一条路径称为一简单路径 (simple path)，如果路径中除起始与终止顶点可以重合外，所有顶点两两不等。
• 行迹（Trace） - 如果路径 P (u,v) 中的边各不相同，则该路径称为 u 到 v 的一条行迹。闭的行迹称作回路（Circuit）。
• 轨迹（Track） - 如果路径 P (u,v) 中的顶点各不相同，则该路径称为 u 到 v 的一条轨迹。闭的轨迹称作圈（Cycle）。
• 桥（Bridge） - 若去掉一条边，便会使得整个图不连通，该边称为桥。

如果图的边没有方向性，则被成为无向图。

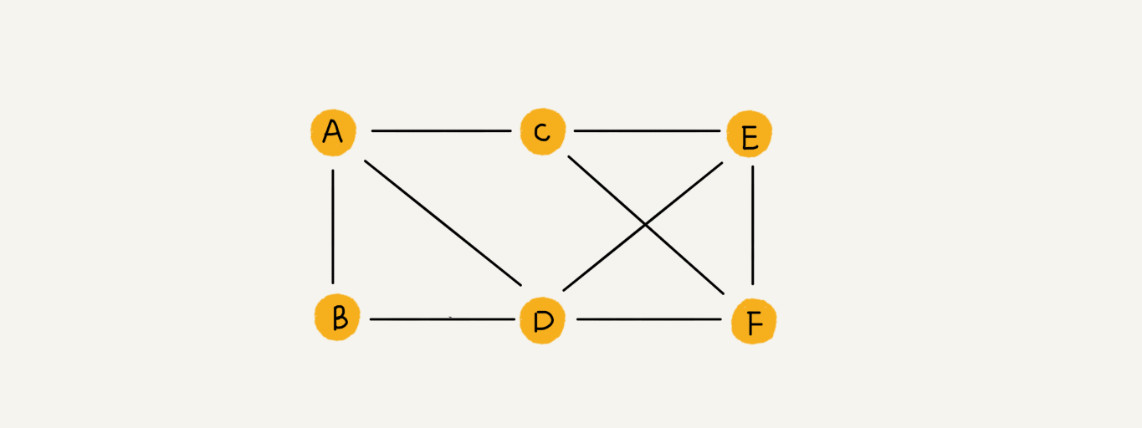
# 图的基本操作

• 创建一个图结构 - CreateGraph (G)
• 检索给定顶点 - LocateVex (G,elem)
• 获取图中某个顶点 - GetVex (G,v)
• 为图中顶点赋值 - PutVex (G,v,value)
• 返回第一个邻接点 - FirstAdjVex (G,v)
• 返回下一个邻接点 - NextAdjVex (G,v,w)
• 插入一个顶点 - InsertVex (G,v)
• 删除一个顶点 - DeleteVex (G,v)
• 插入一条边 - InsertEdge (G,v,w)
• 删除一条边 - DeleteEdge (G,v,w)
• 遍历图 - Traverse (G,v)

# 参考资料

• 数据结构与算法之美